Nessa série de posts comentarei, dentro do meu ponto de vista, o que um bacharel em física deve conhecer até o final de sua graduação. Os objetivos da série são: falar sobre as principais disciplinas da graduação, dar dicas de como estudar, o que estudar e por onde estudar, etc. Em resumo, dar percepção geral sobre o curso de física, para que alunos e vestibulandos possam se beneficiar .
Aviso: Essa série não tem a ambição de ser minuciosa, nem completa, nem de servir como um guia para iniciar pesquisas de ponta em ciência ou no mercado de trabalho. É uma singela lista de conhecimentos elementares para quem quer ter uma rasa noção em ciências físicas e suas aplicações.
No post de hoje comentarei sobre os cursos de Matemática Elementar que poderiam complementar a formação básica do bacharelado em Física…
Introdução
O objetivo deste post é apontar a direção para uma formação mais sólida do física, apontando luz no que parece ser uma das principais lacunas em profissionais de exatas. São disciplinas elementares que possuem uma vasta bibliografia didática. É importante que o físico saia da graduação não apenas executando cálculos, mas entendendo o por que daquelas coisas funcionarem. De nada adianta tentar uma pós graduação em física teórica ou física matemática se não consegue ler os artigos e livros mais relevantes.
É importante entender conceitos de continuidade, suavidade, diferenciabilidade, integrabilidade e convergência de funções em espaços gerais, entender a linguagem de conjuntos, não precisa dominar todo o jargão matemático, mas é importante dominar o básico para compreender definições mais formais e rigorosas. Entender extensões de espaços vetoriais, e quais as propriedades de espaços em dimensão infinita (Para entender Mecânica Quântica, por exemplo), compreender os operadores nesses espaços, como é o espectro deles, suas decomposições e que tipos de aplicações e características importantes eles possuem para teorias físicas (como por exemplo Operadores Unitários, utilizados para propagar no tempo o Estado de um sistema quântico). Conceitos como padrões e simetrias em Física são recorrentes em teorias, os físicos sempre se preocupam em procurar maneiras inteligentes de fazer cálculos, tentando simplificar as operações com propriedades especiais dos sistemas que estão estudando. Abaixo uma lista (incompleta) de disciplinas a serem estudadas na graduação:
Pré Requisitos
Os pré requisitos para essas disciplinas consistem do básico do curso de bacharelado, Cálculo Diferencial e Integral (várias variáveis), Álgebra Linear e Geometria Analítica. Abaixo as sugestões encontram-se mais ou menos na ordem de pré requisitos de um assunto para o outro (exceto para Teoria de Grupos). O curso de Análise na Reta pode ser visto logo após o curso de Cálculo Diferencial e Integral de uma variável real, juntamente com Álgebra Linear.
Análise na Reta
Nessa disciplina o aluno aprende de uma forma mais produtiva a linguagem de conjuntos, se familiariza com os epsilon e deltas, força o raciocínio lógico e dedutivo, aprende a demonstrar teoremas, e estuda conceitos como limites, derivadas e integrais de funções de um ponto de vista não operacional apenas.
Os livros de análise são abundantes, mas vou recomendar apenas um, pelo seguinte motivo: ele foi escrito com o objetivo de compor uma disciplina introdutória de análise na reta, como um minicurso de poucas semanas, e incrivelmente consegue sintetizar o conhecimento de uma maneira pragmática e didática.
Elon Lages Lima, Análise Real Volume 1: Funções de uma variável real, além do livro é possível ver também a vídeo aula ministrada pelo próprio Elon Lages Lima, no site do IMPA é possível assistir as vídeo aulas do Minicurso de Verão de 2011: Análise na Reta.
Análise Real de Várias Variáveis, Análise Vetorial e Análise no Rn
Disciplinas que podem ser resumidas nos cursos do Elon Lages Lima do IMPA. Os livros dele são bem concisos, com exemplos e bastante exercícios. São disciplinas importantes que estudam o cálculo diferencial de várias variáveis, seus teoremas e aplicações. É um bom conjunto de conceitos para carregar na formação a um custo bem baixo, tanto financeiro, pois os livros são bem baratos (devido à excelente iniciativa do IMPA!) e de tempo também, pois o Elon teve o cuidado de escrever livros bem pragmáticos e fáceis de serem estudados.
Elon Lages Lima, Análise no Espaço no Rn, este livro pode ser utilizado como um substituto do Volume 2, do Curso de Análise Real do mesmo auto (logo abaixo). No site do IMPA é possível assistir as vídeo aulas do Programa de Mestrado: Análise no Rⁿ, ministradas pelo próprio Prof. Elon Lages Lima.
Elon Lages Lima, Análise Real Volume 2, trata do estudo do cálculo diferencial e integral de várias variáveis.
Elon Lages Lima, Análise Real Volume 3, trata do estudo da Análise Vetorial. No site do IMPA é possível assistir as vídeo aulas do Programa de Mestrado 2014: Análise Vetorial, ministradas pelo Prof. César Camacho.
Análise Funcional
Nessa disciplina o aluno vai lidar com espaços vetoriais (de funções) em dimensão infinita e em estruturas bem gerais e com diferentes propriedades (normas, topologias, operadores, produto interno, etc.). Para um físico o objeto mais importante em Análise Funcional seria sem muita dúvida os espaços de Hilbert, e entender conceitos como medida de integração, unicidade e existência de soluções de equações diferenciais, e como operadores funcionam nesse espaço (propriedades, espectro, transformações, etc.).
O livro introdutório mais utilizado é o Erwin Kreyszig, Introductory Functional Analysis with Applications. É um livro bem didático, com linguagem simples e boa organização. Tem uma quantidade razoável de exemplos e muitos exercícios (dos quais muitos possuem resposta e resolução completa no final do livro). No site do IMPA é possível ver os vídeos do Curso de Doutorado: Análise Funcional, ministrado pelo Prof. Marcelo Viana. Além do livro do Kreyszig recomendo também o livro Elon Lages Lima, Espaços Métricos.
Geometria Diferencial (GD) e Formas Diferenciais
É muito comum pessoas ingressarem num curso de física por causa do Einstein e de sua Teoria da Relatividade Geral (RG), e para que um curso de RG seja proveitoso, essa disciplina de Geometria Diferencial (GD) deveria ser um pré requisito. Para poder atacar grandes referências como o livro do Wald, se faz necessário um pouco mais de maturidade e sofisticação em se tratando de ferramental matemático. Novamente, a literatura é abundante, eis algumas sugestões de livros:
Manfredo Perdigão do Carmo, Differential Geometry of Surfaces and Curves, este livro possui uma versão em português no site da SBM. No site do IMPA é possível baixar os vídeos do Curso de Mestrado: Geometria Diferencial, ministrado pelo Prof. Fernando Codá. O livro do Manfredo é bem didático, tem uma quantidade razoável de exemplos, e bastante exercícios (com respostas e dicas no final do livro). Além disso, assim como o Elon Lima, o Manfredo tem uma escrita e didática muito boa, conseguindo linearizar bem os capítulos.
Além do livro do Manfredo de Geometria Diferencial, também recomendo o livro dele de formas diferenciais: Manfredo Perdigão, Differential Forms and Applications.
Teoria de Grupos
Nesse assunto devo admitir ignorância, pois nunca estudei propriamente (de uma forma rigorosa e formal). Meu conhecimento é fragmentado e com viés de Teoria Quântica, pois todo o (raso) conhecimento que adquiri nesse assunto foram em livros “De físicos para físicos”, ou seja com mais aplicações diretas e específicas do que definições e demonstrações de teoremas.
Minha primeira recomendação seria o curso do Prof. Guilhermo Cabrera de Teoria de Grupos Aplicada à Física, ele disponibilizou um material muito rico em sua página, e com certeza foi um dos melhores professores que já tive (recomendo o curso dele de Física Estatística!). Na página do Prof. Cabrera existem diversas referências didáticas e avançadas.
Para os físicos, é muito importante estudar os Grupos de Lie, suas transformações de ponto, e suas simetrias. É sem dúvida fundamental para quem quer entender Mecânica Clássica e Mecânica Quântica, a álgebra de operadores e as formulações Hamiltonianas. Eu pessoalmente fiquei muito feliz depois que entendi que a Derivada de Lie tinha conexão com álgebra de Momento Angular na Mecânica Quântica, e que o produto vetorial é na verdade um Grupo de Lie, e que isso abre uma “caixa de pandora” para um monte de coisas divertidas como spinores, tensores, formas diferenciais e explica um monte de coisa em Relatividade Geral, por exemplo! Outra aplicação muito legal são simetrias em equações diferenciais (estudei isso no meu primeiro Doutorado, que tranquei para trabalhar no mercado financeiro). O Sophus Lie realmente foi um cara primordial para a Matemática e para a Física. Ele desbravou e abriu clareiras para diversos ramos de estudo!
Eu comecei a ver no site do IMPA, Programa de Doutorado 2012:Lie Groups, Representation Theory and Symmetric Spaces, então não posso garantir se esse curso seria proveitoso para um físico, pois estou no início ainda, mas de qualquer forma vale a pena deixar aqui a existência desse curso. Tem também essa daqui Introduction to Lie Algebras, pelo Prof. Reimundo Heluani.
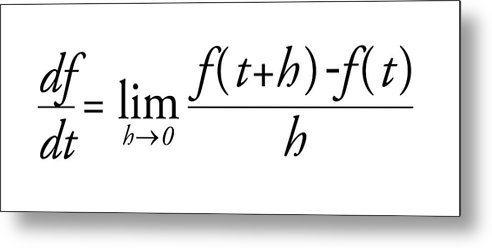
Comentários